Um cilindro circular reto é inscrito em um cone com altura e raio da base . Encontre o maior volume possível para este cilindro.
Passo 1
Oi, pessoal! Tudo certinho?
O enunciado pediu pra gente encontrar o maior volume possível para um cilindro inscrito em um cone com altura e raio da base
Temos aqui um problema de máximos e mínimos! Especificamente de máximo, então vamos resolver derivando uma função e igualando à zero, beleza?
Mas antes disso, saca esse esqueminha que vai nos ajudar a obter a função para o volume que queremos maximizar.
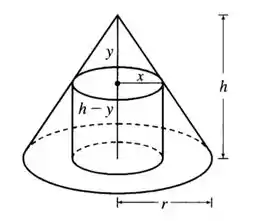
Para resolver essa questão, vamos precisar usar a fórmula do volume do cilindro e tentar escrevê-la em função de apenas uma variável (usando as relações do triângulo que aparece na figura).
Em seguida, vamos encontrar os pontos críticos dessa função e o valor máximo para o volume deste cilindro.
Bora lá?
Passo 2
Para o volume de um cilindro temos a seguinte fórmula:
Mas observe a figura e perceba que a altura do cilindro é , e que o raio pode ser escrito como . Assim, temos:
Aplicando a propriedade distributiva nesse produto:
Passo 3
Na Figura, temos um caso de semelhança de triângulos!
Podemos comparar o raio do cone com o raio do cilindro, e a altura do cone com a altura formada pelo triângulo retângulo menor.
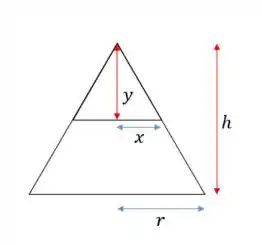
Primeiro, usamos a semelhança para isolarmos uma das variáveis.
Como
então
Substituindo a variável isolada na expressão do volume
temos que
Passo 4
Precisamos calcular a derivada da função
para encontrar os seus pontos críticos. Para isso, vamos usar a Regra da Potência em cada um dos seus termos. Relembrando a Regra da Potência:
Agora, calculando a derivada de em relação a :
Igualando essa expressão a zero:
Isolando o termo :
Assim, pra que esse produto seja verdadeiro, devemos ter:
ou
Mas pensa só, o raio não pode ser zero, né? Então não é uma boa solução. Usando a outra opção, vamos ter:
Simplificando temos
e isolando :
Assim, temos dois pontos críticos, mas pra temos , então o ponto máximo deverá ser .
Passo 5
Por fim, vamos encontrar o volume máximo para a função
Para isso, só precisamos substituir o encontrado no Passo 4 na equação do volume. Assim:
então
Dessa forma:
Prontinho, galera!
Até a próxima! 😉
Resposta
O maior volume possível para o cilindro inscrito em um cone com altura e raio da base é: