Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.4 - Ex. 25
Suponha que os gráficos de e foram traçados sobre uma malha coordenada com . Mostre que, a uma distância de à direita da origem, a altura do gráfico de é de , enquanto a altura do gráfico de é cerca de
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente mostrar que a uma distância de à direita da origem, a altura do gráfico de é de , enquanto a altura do gráfico de é cerca de , sabendo que os gráficos de e foram traçados sobre uma malha coordenada com .
Confuso né??
Em outras palavras, temos que imaginar um plano coordenado de forma que cada unidade representa . O exercício quer que andemos pra direita, ou seja, unidades de .
Vamos dar uma olhada no gráfico dessas funções:
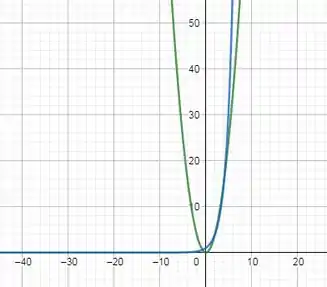
Podemos perceber que conforme aumentamos o valor de , a função cresce mais rápido do que a função de .
Isso já nos indica que quando andarmos unidades para a direita, o valor de vai ser bem maior do que o valor de .
Agora vamos verificar cada gráfico!! 😉
Passo 2
Beleza, agora vamos calcular o valor das funções para . Para :
Aqui, como a unidade está em centímetros, podemos transformar para metros:
Então, a altura da função quando andamos para a direita é de .
Passo 3
Agora para :
Aqui, como a unidade está em centímetros, podemos transformar para quilômetros:
Podemos ver como próximo a , então:
Então, a altura da função quando andamos para a direita é de .
Entendeu direitinho?? Responde aee 😉