Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.3 - Ex. 4 b
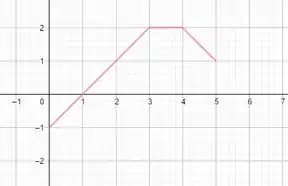
É dado do gráfico de Esboce os gráficos das seguintes funções:
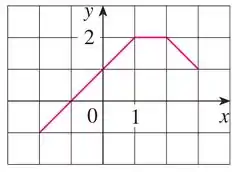
b)
Passo 1
Fala aí! como vai?
Nesse problema foi dado um gráfico de uma função
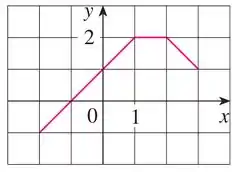
E nosso objetivo é esboçar o gráfico de a partir de .
Parece complicado?
Para resolver o problema temos que lembrar que quando somamos ou subtraímos no argumento de uma função, estamos transladando a função horizontalmente.
Dessa forma, usando como base, podemos esboçar apenas transladando horizontalmente para a direção correspondente.
Veja só!
Passo 2
Não acredita em mim? Vamos fazer um teste...
No gráfico de , qual o valor em ?
, não é?
Mas na função , qual será o valor em ? , não é? Ou seja
Viu só o que aconteceu? Transladamos a função duas unidades para a esquerda...
Isso sempre vai acontecer... quando subtraímos um valor do argumento de uma função , transladamos o gráfico de unidades para a direita.
(OBS: Se for somado ao argumento de , a translação acontecerá para a esquerda)
No nosso caso, então, só deslocar 2 unidades para a direita. Vamos lá!
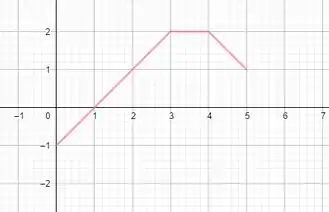
E aí! entendeu tudo? Responde Aí!
Resposta
