Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 12
Suponha que seja diferenciável em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.
12.Se então será crescente em .
Passo 1
Não necessariamente! Peguemos alguns exemplos de funções em que seja maior que 0:
:
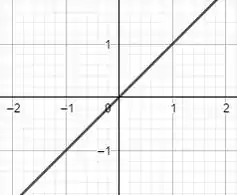
Onde , que é maior que 0, e é crescente no intervalo . Outro exemplo:
:
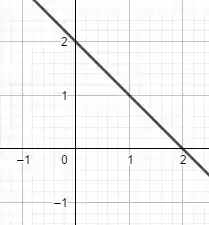
Onde , também, e agora é decrescente, no mesmo intervalo.
Passo 2
Assim, nossa conclusão é que a afirmação não é necessariamente verdadeira, por existirem exemplos a favor e contra ela. Logo, consideraremos como falsa.
Resposta
Falsa.
Exercícios de Livros Relacionados
Demonstre que funções crescentes e decrescentes são injetoras. Ou seja, demonstre que, para quaisquer x 1 e x 2 em I , x 1 ≠ x 2 implica f x 2 ≠ f x 1
Use os resultados do Exercício 81 para mostrar que a função apresenta inversa em seu domínio. Determine uma fórmula para d f - 1 / d x usando o Teorema 3 da Seção 3.8. f x = 1 - 8 x 3
Use os resultados do Exercício 81 para mostrar que a função apresenta inversa em seu domínio. Determine uma fórmula para d f - 1 / d x usando o Teorema 3 da Seção 3.8. f x = 1 - x 3
Use os resultados do Exercício 81 para mostrar que a função apresenta inversa em seu domínio. Determine uma fórmula para d f - 1 / d x usando o Teorema 3 da Seção 3.8. f x = 1 3 x + 5 6
Use os resultados do Exercício 81 para mostrar que a função apresenta inversa em seu domínio. Determine uma fórmula para d f - 1 / d x usando o Teorema 3 da Seção 3.8. f x = 27x 3