Suponha que seja diferenciável em toda parte. Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.

13.Se for crescente em , então .

Teoremas do Cálculo – que não precisamos nos aprofundar aqui no momento – comprovam que, quando uma função é crescente em um determinado intervalo, a derivada é necessariamente positiva e não nula.

Você pode imaginar e interpretar isso como uma linha reta com inclinação positiva (no sentido anti-horário). Um exemplo fácil de função que contempla esse teorema e a afirmação é:

:

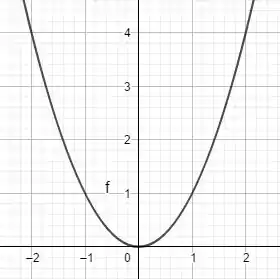
Lembre-se que pra derivada se anular, essa linha reta, tangente ao gráfico, precisa estar paralela ao eixo , horizontal. Nessa função, crescente no intervalo , isso só ocorre em .

Temos que a afirmação é verdadeira.