Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.4 - Ex. 27
Suponha que para o tanque do Exercício 21, a bomba quebre depois de o trabalho de J ter sido realizado. Qual é a profundidade da água remanescente no tanque?
Passo 1
Faremos o seguinte esboço:
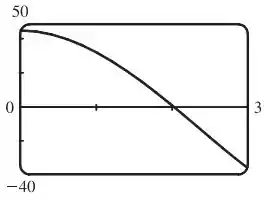
Se apenas J é feito, então a apenas a água sobre um certo nível (chamaremos de ) será bombeada. Então nós usaremos a fórmula do Exercício 21, exceto que o trabalho é fixado e estamos tentando achar o limite inferior da integração:
Passo 2
Para encontrar a solução dessa equação, nós colocamos entre e . Nós vemos que a equação é satisfeita para Portanto, a profundidade da água que permanece no tanque é de cerca de .
Resposta
.
Exercícios de Livros Relacionados
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: y = x ; y = 2 x ; y = 2
Você é o responsável pela drenagem e pelo reparo do tanque de armazenamento mostrado a seguir. O tanque é um hemisfério com raio de 10p é s é , cheio de benzeno, cujo peso específicoé 56 l b p é 3 é .
Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Nos exercícios 23 e 24 use a densidade da água igual a 62,5l b / p é 3 é .
Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Use a densidade da água igual a 62,5l b / p é 3 é .
Resolva o exercício 22 se o tanque estiver com a metade de óleo, que tem densidade de 920k g / m 3 .Exercício 22 : Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela