Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.4 - Ex. 24
Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Use a densidade da água igual a .
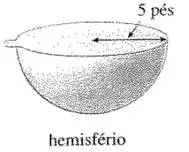
Passo 1
Vamos supor que a altura da água seja . Então qual é a área de um pequeno “disco” de água nessa profundidade?
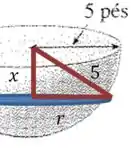
Então a massa desse pequeno disco é:
Passo 2
E o trabalho realizado para cada um desses “discos de água”:
E agora integrando com variando de até pés:
Então o trabalho é:
Resposta
O trabalho necessário é .
Exercícios de Livros Relacionados
Uma piscina circular tem um diâmetro de 10 m, os lados têm 1,5 m de altura e a profundidade da água é de 1,2 m. Quanto trabalho é necessário para bombear toda a água pelo lado da piscina? (Use o fato
Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Nos Exercícios 23 e 24 use a densidade da água igual a 62,5 lb/pé³.
Suponha que para o tanque do Exercício 21, a bomba quebre depois de o trabalho de 4,7 × 10 5 J ter sido realizado. Qual é a profundidade da água remanescente no tanque?
Resolva o Exercício 22 se o tanque estiver cheio até a metade de óleo, que tem densidade de 900 kg/m³.