Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.4 - Ex. 26
Resolva o exercício se o tanque estiver com a metade de óleo, que tem densidade de .
Exercício : Um tanque está cheio de água. Encontre o trabalho necessário para bombear a água pela saída. Use a densidade da água igual a .
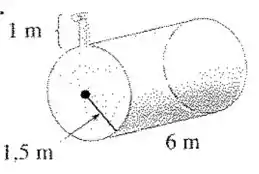
Passo 1
Já que o tanque está cheio pela metade, estamos na verdade lidando com algo parecido com o seguinte:
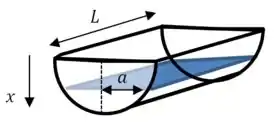
Precisamos de uma função que dê a massa de cada um desses pequenos “retângulos de água”, já que a expressão para o trabalho necessário para bombear um deles é:
Se cada um desses “retângulos” tem uma espessura , então:
E pelo desenho podemos dizer que a área é:
A largura do retângulo é constante, mas o comprimento varia junto com a “profundidade” . Podemos escrever em função de se lembrarmos da equação para esse trecho da circunferência de raio :
Então a nossa fórmula é:
E a altura pela qual esse “retângulo” deve ser erguida é a profundidade somada ao da metade superior do tanque, somada ao comprimento de do cano.
Passo 2
Ok, já temos o trabalho necessário para bombear um pequeno “retângulo” de espessura para fora do tanque, quando ele está localizado a uma profundidade .
Para calcular o trabalho total, só precisamos integrar essa expressão com variando de até :
Vamos separar essa integral em duas:
Agora preciamos resolver cada uma delas.
Passo 3
Vamos começar com a integral da esquerda:
Aqui estamos pegando a equação para a parte de cima de uma circunferência de raio e integrando ela quando vai de até :
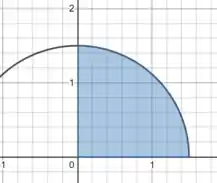
Ou seja, estamos simplesmente calculando a área de um quarto de círculo de raio !
Passo 4
Agora vamos olhar para a integral da direita:
Essa já não tem um significado geométrico tão óbvio. Então vamos tentar uma substituição:
Então, substituindo as variáveis e os limites de integração:
Para nos livrarmos daquele sinal, vamos trocar a ordem dos limites de integração:
Passo 5
Agora vamos voltar à nossa equação para o trabalho total:
Substituindo os resultados que já calculamos:
Resposta
O trabalho necessário é de .