Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 37
A tabela dá o consumo de potência em megawatts, em Ontário, da meia-noite até às horas da manhã em de dezembro de . Use a Regra de Simpson para estimar a energia usada durante aquele período. (Utilize o fato de que a potência é a derivada da energia.)
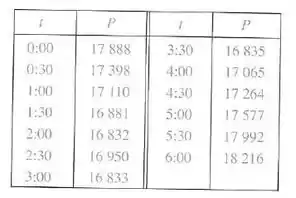
Passo 1
Temos o intervalo , e vamos usar , temos que :
Com a Regra de Simpson é usado parábolas ao invés de segmentos de reta para aproximar a curva, assim a fórmula fica com um padrão , , , , . . . , , , , :
Resposta
A energia estimada usada durante aquele período foi de megawatt-hora.
Exercícios de Livros Relacionados
Quão grande deve ser n para garantir que a aproximação pela Regra de Simpson de ∫ 0 1 e x 2 d x tenha uma precisão de 0,00001 ?
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 4
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0
Use (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson para aproximar a integral dada com o valor especificado de n . (Arredonde seu resultado para seis casas decimais.) ∫ 0