Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.4 - Ex. 6c
A tabela fornece a população dos Estados Unidos, em milhões, para os anos .
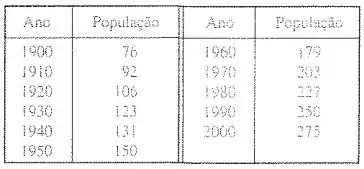
Desenhe um gráfico mostrando ambas as funções exponenciais das partes (a) e (b) juntas com o gráfico da população real. Esse modelos são razoáveis?
Passo 1
Nos itens (a) e (b) achamos funções exponenciais que descrevem a população americana em função do tempo:
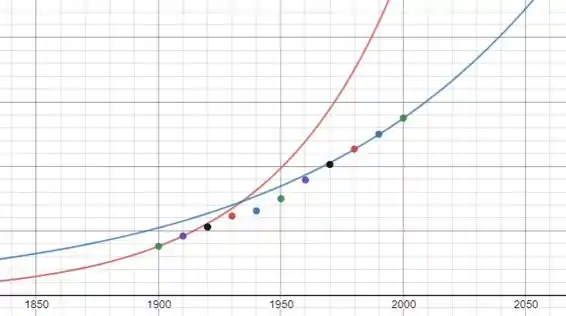
A seguir plotamos as duas curvas e os pontos da tabela:
Passo 2
Note que a curva vermelha (item a) descreve bem apenas os primeiro pontos, já que ela foi ajustada com eles. Já a curva azul (item b), por sua vez, ajusta muito bem os últimos pontos. Notamos então que houve uma mudança na taxa de crescimento ao longo do século XX: a taxa de crescimento da população diminuiu com o passar do tempo!
Resposta
Esboço.
Exercícios de Livros Relacionados
Uma equação diferencial da forma d y d x = f a x + b y + c ,b ≠ 0 , pode sempre ser reduzida a uma equação com variáveis separáveis por meio da substituição u = a x + b y + c . Use este procedimento p
Nos problemas 1-40, resolva a equação diferencial dada por separação de variável.35. d y d x = s e nx . cos 2 y - c o s 2 y
Nos problemas 1-40, resolva a equação diferencial dada por separação de variável.40. x + x . d y d x = y + y
Nos problemas 49 e 50, encontre uma solução para a equação diferencial dada que passe pelos pontos indicados.50. x d y d x = y 2 - y a) (0, 1)
Nos problemas 41-48, resolva a equação diferencial dada sujeita à condição inicial indicada.43. y d y = 4 x y 2 + 1 1 2 d x , no qual y 0 = 1 .