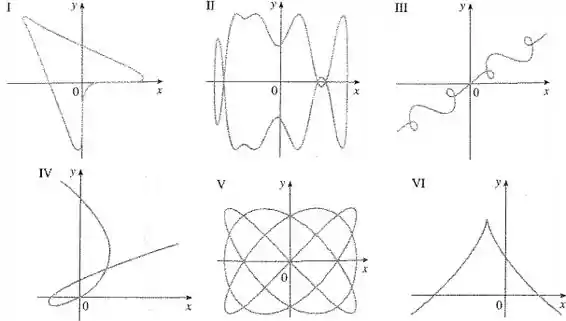
Ligue as equações paramétricas aos gráficos de I-VI.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade juntos.
A questão fornece uma curva parametrizada e pede para identificarmos o seu gráfico.
Nesse caso, a curva é:
Para corresponder o gráfico com as funções, precisamos observar como as funções se comportam em alguns valores especiais.
Podemos olhar as raízes, os limites para analisar o que ocorre com o crescimento e o decrescimento de , devemos observar esses pontos e assim poderemos escolher o gráfico que melhor se enquadra.
Passo 2
Desta forma, tanto quando
como quando
explode para .
A única curva que faz isso é a .
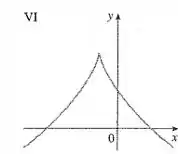
Note também que se fizermos
obtemos apenas
a curva só intercepta o eixo em um ponto.
Por outro lado, se fizermos
achamos
a curva corta o eixo em dois pontos distintos! É exatamente isso que o gráfico VI faz!