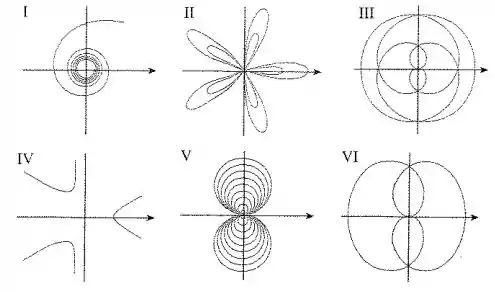
Conecte as curvas polares com seus respectivos gráficos I-VI.
Passo 1
A questão pede para ligarmos a curva dada em coordenadas polares a um dos gráficos disponíveis.
Neste caso, temos
Bom, essa é uma curva que parece ser bem estranha pois mistura uma função trigonométrica com um polinômio...
Passo 2
Observe que conforme aumenta, a amplitude de vai sempre aumentando, porém ela é modulada pelo . Assim, sempre que , . Portanto, devemos ter uma curva cujo comportamento vai se repetindo eternamente, porém sempre com maior amplitude! Bingo: curva V.
Resposta
V