Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.6 - Ex. 28
Um tanque cilíndrico com 3 m de altura e 1,5 m de raio está sobre uma plataforma a 15 m de altura. Ache a profundidade da água quando foi a metade do trabalho necessário para encher o tanque realizada através de cano que vai do nível do solo à base do tanque.
Passo 1
Queremos aqui saber quanto de água foi colocada no tanque se realizamos só metade do trabalho necessário para encher tudo, trazendo a água da altura do solo. Sabemos que o trabalho realizado para levantar uma massa de água em uma altura é dado por , sendo a massa de água e o valor da aceleração da gravidade. Devemos então primeiro integrar a expressão , sendo a massa de cada “disco” de água que possui altura e a área igual à da base do cilindro, para achar o trabalho total que deve ser realizado para bombear toda a água.
Passo 2
Colocaremos o eixo apontado para cima e com origem na base do tanque. Cada disco infinitesimal de água terá uma altura e uma área igual a área da base do cilindro m².
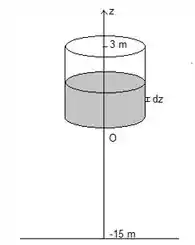
O volume do elemento é então . Como a densidade da água é 1000 kg/, a massa de cada elemento é então . Além disso, cada elemento de água que está em uma posição , com indo de 0 m, a 3 m, deve ser erguido m. Assim obtemos a expressão .
Passo 3
Agora podemos integrar para obter , com indo de 15 m até o topo do tanque em 18 m.
Passo 4
Agora temos o trabalho total necessário para bombear água pro tanque inteiro. Mas o trabalho realizado foi apenas metade do necessário, então temos:
Já vimos que se quisermos bombear água até uma altura devemos realizar um trabalho dado por:
Então, realizando um trabalho :
Temos então a equação de segundo grau:
Passo 5
Resolvendo a equação para :