Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 12
Um tanque grande é projetado com as extremidades no formato da região entre as curvas e , medidas em pés. Calcule a força hidrostática em uma extremidade do tanque se ele estiver cheio até uma profundidade de pés com gasolina. (Suponha que a densidade da gasolina seja .)
Passo 1
Com as informações do enunciado a gente forma a seguinte figura:
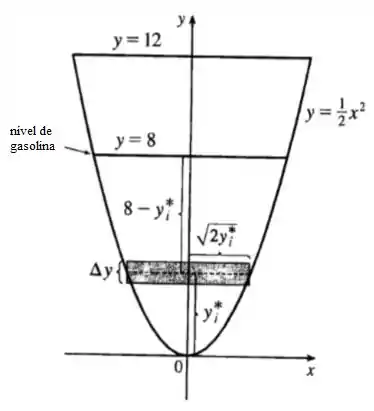
A área da faixa retangular é , e a pressão nela é .
Passo 2
A força total é
Resposta
.
Exercícios de Livros Relacionados
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
3. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é submersa (ou parcialmente submersa) em água e tem o formato indicado. Explique como aproximar a força hidrostática contra um lado da placa por uma soma de Riemann. Então expresse
5. Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann.
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent