Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 21
As massas pontuais estão localizadas no eixo conforme mostra a figura a seguir. Ache o momento do sistema com relação à origem e o centro de massa .
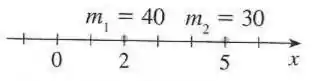
Passo 1
O momento do sistema com relação à origem é
Passo 2
A massa do sistema é .
Passo 3
O centro de massa do sistema é .
Resposta
Momento:
Centro de massa:
Exercícios de Livros Relacionados
Expresse o limite como uma integral definida no intervalo dado. lim n → ∞ ∑ i = 1 n x i * x i * 2 + 4 . ∆ x [ 1 ,3 ]
Use a regra do ponto médio como o valor dado n = 4 para aproximar a integral ∫ 1 5 x 2 e - xd x . Arredonde cada resposta para quatro casas decimais.
Use a regra do ponto médio como o valor dado n = 4 para aproximar a integral ∫ 0 8s e nx d x . Arredonde cada resposta para quatro casas decimais.
É dado o gráfico de uma função f .Estime ∫ - 2 4 f x d x usando seis subintervalos com Extremidades direitas.
É dado o gráfico de uma função f .Estime ∫ 0 10 f x d x usando cinco subintervalos com Pontos médios