Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 6.2 - Ex. 12a
Um tanque tem a forma de um paralelepípedo retângulo cuja base tem dimensões 1m e 2m e cuja altura é 1,5m. O tanque está cheio de uma substância com densidade variável. Em cada ponto, a densidade é proporcional à distância do ponto até a superfície superior do tanque.
- Determinar a função que define o campo de densidade.
Passo 1
Beleza galera, vamos olhar este retângulo mais de perto:
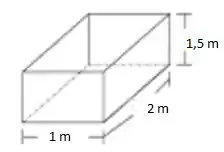
Então, a distância de um ponto P até a superfície será dada pela altura total menos a distância z até o fundo.
Sendo assim, a distância de P à superfície será:
Como a densidade é proporcional à distância:
Para podermos achar uma igualdade devemos acrescentar uma constante:
E assim terminamos a letra (a) !!
Resposta
Exercícios de Livros Relacionados
A curvatura da curva C mostrada na figura é maior em P ou em Q ? Explique.Estime a curvatura em P e Q desenhando o círculo osculador nesses pontos.
Dois gráficos, a e b , são mostrados. Um é a curva y = f ( x ) e o outro é o gráfico da função curvatura y = κ ( x ) . Identifique cada uma e justifique suas escolhas.
Use o Teorema 10 para mostrar que a curvatura da curva plana parametrizada x = f t , y = g ( t ) , é κ = x ˙ y ¨ - y ˙ x ¨ x ˙ 2 + y ˙ 2 3 / 2
Dois gráficos, a e b , são mostrados. Um é a curva y = f ( x ) e o outro é o gráfico da função curvatura y = κ ( x ) . Identifique cada uma e justifique suas escolhas.
Use a Fórmula 11 para encontrar a curvatura. y = 4 x 5 / 2