Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.3 - Ex. 38
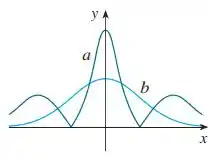
Dois gráficos, e , são mostrados. Um é a curva e o outro é o gráfico da função curvatura . Identifique cada uma e justifique suas escolhas.
Passo 1
Olá, meu querido e amado aluno. Vou te ajudar a entender e resolver essa atividade.
A gente tem o gráfico abaixo:
E deveremos identificar quem é o gráfico de:
E quem é o gráfico da função curvatura:
Dada uma curva de função a curvatura será dada por:
Passo 2
Analisando, se a curva fosse , sua curvatura teria picos quando a função vai pra , o que não acontece na curva .
Por outro lado, a curva de tem uma mudança de comportamento em questão da concavidade, que é calculado pela segunda derivada, o que faz a função concavidade zerar, que acontece justamente onde a curva zera, portanto
Resposta
Exercícios de Livros Relacionados
Encontre os vetores T , N e B no ponto indicado.r (t) = (t^2 , (2)/(3) t^3 , t) (1 , (2)/(3) , 1)
Em que ponto a curva tem curvatura máxima? O que acontece com a curvatura quando x → ∞ ? y = e x
Determine as equações para o círculo osculador da elipse 9 x 2 + 4 y 2 = 36 nos pontos ( 2,0 ) e ( 0,3 ) . Utilize uma calculadora gráfica ou computador para traçar a elipse e ambos os círculos oscula
Em que ponto a curva x = t 3 , y = 3 t , z = t 4 o plano normal é paralelo ao plano 6 x + 6 y - 8 z = 1 ?
Encontre as equações para o círculo osculador da parábola y = 1 2 x 2 nos pontos ( 0,0 ) e 1 , 1 2 . Trace os dois círculos osculadores e a parábola na mesma tela.