Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 10
The Fitzhugh-Nagumo model for the electrical impulse in a neuron states that, in the absence of relaxation effects, the electrical potential in a neuron obeys the differential equation
where a is a positive constant such that
Passo 1
- Para que valores de está descarregado, ou seja
- Para que valores de está crescendo
- Para que valores de está decrescendo
Bem, temos uma questão interdisciplinar, sobre o potencial elétrico de um neurônio. Primeiramente temos que manipular nossa equação
Só aqui já achamos um valor v pois temos aquela regrinha de matemática básica
Então temos que v pode ser
Ou
Ou seja podemos ter
Passo 2
Para nosso Potencial estar crescendo, temos o seguinte requisito
Então agora precisamos achar esse intervalo
A mesma regra que eu falei la em cima vale aqui também
E também que :
Passo 3
Para nosso Potencial estar decrescendo, temos o seguinte requisito
Então agora precisamos achar esse intervalo
A mesma regra que eu falei la em cima vale aqui também
E também:
Se formos montar uma tabela ela ficaria assim
Se formos plotar um gráfico seria assim
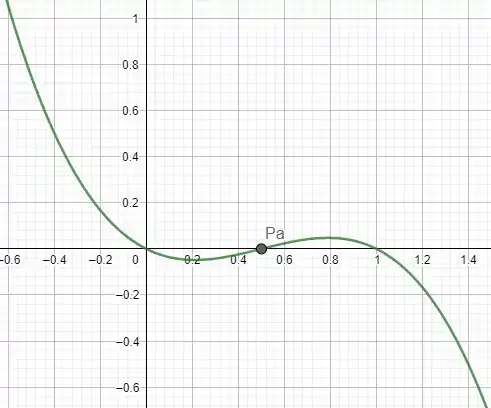
Prontinho. Conseguimos demonstrar que é solução. Terminamos por aqui. Te vejo na próxima resolução : )
Resposta
Ei, a resposta está no passo a passo :)