Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 47
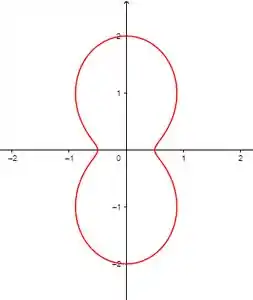
A figura mostra o gráfico de como uma função de em coordenadas cartesianas. Use-o para esboçar a curva polar correspondente.
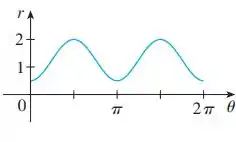
Passo 1
Oii, tudo certinho contigo??
Bom... o enunciado nos deu o seguinte gráfico de como uma função de em coordenadas cartesianas:
Queremos esboçar a curva polar correspondente.
Lembre-se que nas equações polares o representa a distância do ponto até a origem e o a angulação deste ponto em relação ao eixo no plano.
Nesta questão vamos ter que pegar uma aproximação dos valores e fazer o esboço do gráfico com eles à medida que o ângulo aumenta.
Passo 2
Analisando a função, no primeiro quadrante ela começa em e sobe até , então no segundo ela desce de até e esse padrão se repete nos próximos dois quadrantes, veja:
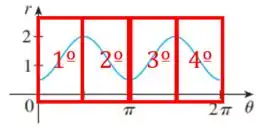
Colocando no gráfico a gente tem que representar esses aumentos e diminuições do em distancia a mediada que o ângulo muda.
Assim, a curva polar é dada da seguinte forma:
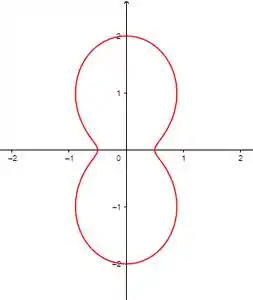
Resposta
