Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 47
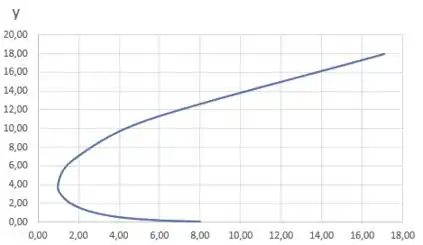
Trace a curva e calcule seu comprimento.
46.
Passo 1
Eaee, tudo tranquilo?? Bom... o enunciado nos deu as seguintes expressões de uma curva parametrizada:
Em que pertence ao seguinte intervalo:
Queremos esboçar a curva que tem as equações paramétricas dadas.
Para fazer isso, vamos criar uma tabelinha de valores que relacionam e, aí poderemos plotar esses pontos no gráfico.
Já para calcular o seu comprimento , basta saber que o comprimento é dado pela seguinte integral:
Com isso, basta derivarmos as equações e aplicar nessa expessão!! 😉
Passo 2
Primeiramente vamos plotar o gráfico...
Para isso, vamos utilizar alguns valores dentro do intervalo dado de e verificar os valores para e .
Assim, quando , por exemplo, teremos e .
Fazemos o mesmo para outros valores de e montamos a seguinte tabela:
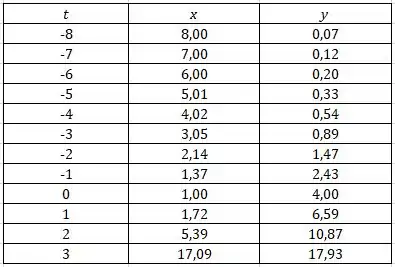
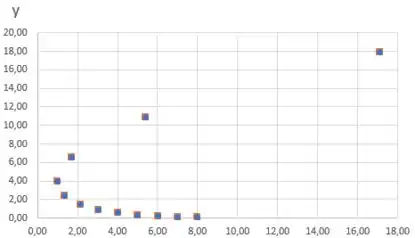
Show! Colocando esses pontos em um gráfico, obtemos:
Agora, traçando uma linha, obteremos a curva que desejamos:
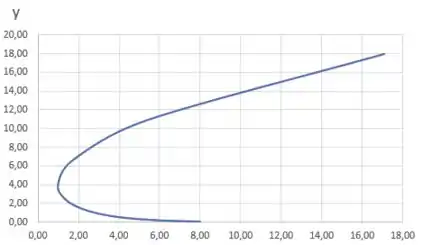
Passo 3
Agora nós queremos calcular o comprimento dessa curva. Sabemos que o comprimento de uma curva pode ser calculado pela integral:
Então mãos à obra! Vamos calcular e .
Para isso, sabemos que a derivada da exponencial é a própria exponencial. Com isso, poderemos calcular a primeira derivada:
Aplicando o mesmo conhecimento, juntando com a Regra da Cadeia, podemos resolver a derivada de :
Passo 4
Assim, substituindo os valores na integral e simplificando, temos:
Resolvendo a integral, temos:
Aplicando os limites de integração:
Então o comprimento dessa curva é
Resposta
