Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 58

Escreva, mas não calcule, uma integral que represente a área da superfície obtida pela rotação da curva dada ao redor do eixo x.

57. x = s e n 2 t ,       y = s e n   3 t ,         0 ≤ t ≤ π / 3

Passo 1

Precisamos escrever uma integral que represente a área da superfície obtida pela rotação da curva dada ao redor do eixo x .

Sabemos que a área de uma superfície é

S = ∫ a b 2 π y   d s

Sendo que

d s =   d x d t 2 + d y d t 2

Vamos primeiro dar uma olhada na região que precisamos trabalhar:

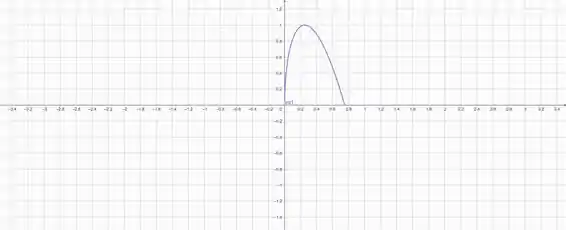
Então basicamente vamos girar essa superfície em torno do eixo x . Precisamos então calcular as derivadas das parametrizações e precisamos depois disso montar a integral.

Passo 2

Vamos começar então com a derivada de x :

d x d t = d sin 2 ⁡ t d t

Como a gente tem uma composição de funções aqui, a gente vai precisar utilizar a regra da cadeia:

d x d t = d d u u 2 ⋅ d d t sin ⁡ t

d x d t = 2 sin ⁡ t cos ⁡ t

Beleza, agora a gente vai partir para a derivada de y :

d y d t = d sin ⁡ 3 t d t

Por termos outra composição de função, a gente precisa aplicar a regra da cadeia aqui:

d y d t = d 3 t d t ⋅ d d u sin ⁡ u

d y d t = 3 t ⋅ cos ⁡ 3 t

Então a gente já pode começar a montar a integral:

S = ∫ a b 2 π y   d s

d s =   d x d t 2 + d y d t 2

d s = 4 sin 2 ⁡ t cos 2 ⁡ t + 9 t 2 cos 2 ⁡ 3 t

S = ∫ a b 2 π sin ⁡ 3 t 4 sin 2 ⁡ t cos 2 ⁡ t + 9 t 2 cos 2 ⁡ 3 t d t

Resposta

S = ∫ a b 2 π sin ⁡ 3 t 4 sin 2 ⁡ t cos 2 ⁡ t + 9 t 2 cos 2 ⁡ 3 t d t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as coordenadas do centróide da curva:x = c o s t + t s e n t , y = s e n t - t c o s t , 0 = t = pi // 2 .
Cicloidea. Encontre o comprimento de um arco da ciclóide x = a ( t - s e nt ) ,y = a ( 1 - c o s t ) b. Encontre a área da superfície gerada ao girar um arco da ciclóide no item (a) em torno do eixo x
a. Mostre que a fórmula cartesiana L = ∫ c d 1 + d x d y 2 d y para o comprimento da curva x = g ( y ) ,c ≤ y ≤ d (Seção 6.3, Equação 4), é um caso especial da fórmula paramétrica para comprimento L =
Encontre as áreas das superfícies geradas girando as curvas nos Exercícios 31-34 em torno dos eixos indicados.34. x = l n ( s e c t + t gt ) ,y = c o st ,0 ≤ t ≤ π / 3 ,e i x ox
Encontre as coordenadas do centróide da curva:x = e^t c o s t , y = e^t s e n t , 0 = t = pi .