Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 52
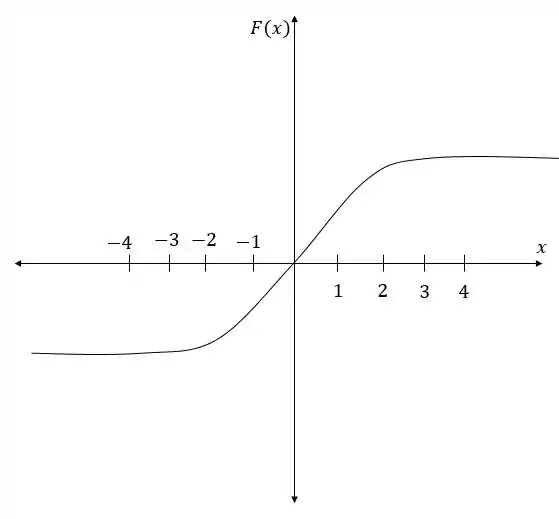
Trace um gráfico de e então o use para fazer um esboço da antiderivada que passe pela origem.
Passo 1
Usando uma calculadora, podemos mostrar o gráfico de no intervalo dado:
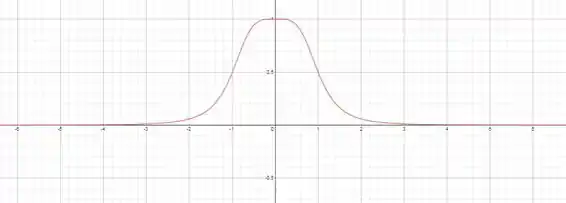
Se é a antiderivada de , então , e estamos olhando para o gráfico da inclinação de . Com isso, conseguimos estimar como se comporta a função .
Passo 2
Podemos ver que a inclinação do gráfico é zero quando , então temos assíntotas horizontais dos dois lados. A inclinação começa a crescer próxima do e vai até 1 em , onde é fica quase constante em um trecho. Depois a inclinação começa a cair novamente indo a zero. Posicionando o gráfico para passar na origem, o esboço do gráfico fica então assim:
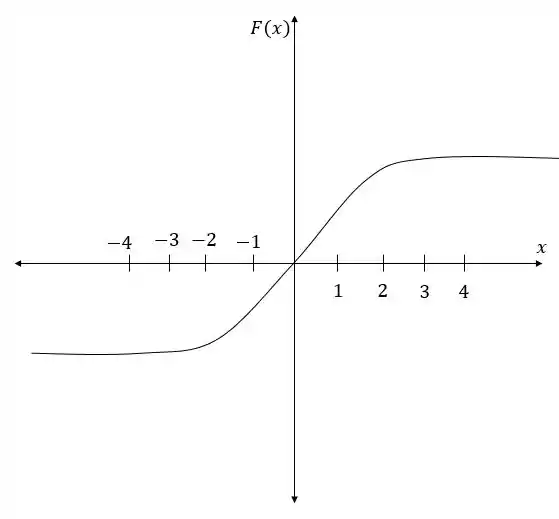
Resposta
Exercícios de Livros Relacionados
Qual dos gráficos a seguir mostra a solução do problema de valor inicial d y d x = 2 x ,y = 4q u a n d ox = 1 ? Justifique sua resposta.
Diga se cada uma das fórmulas está certa ou errada e justifique em poucas palavras.
Diga se cada uma das fórmulas está certa ou errada e justifique em poucas palavras.
Certo ou errado? Justifique em poucas palavras.
Diga se cada uma das fórmulas está certa ou errada e justifique em poucas palavras.