Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.10 - Ex. 51
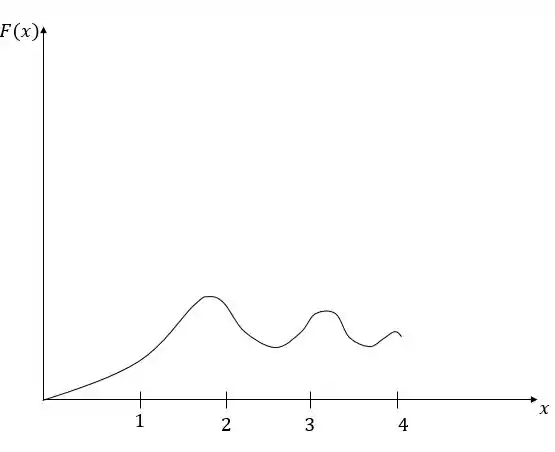
Trace um gráfico de e então o use para fazer um esboço da antiderivada que passe pela origem.
Passo 1
Fala aí, belezinha?
Bom, nessa questão estamos interessados em traçar um gráfico para a primitiva da função
Para isso, iremos utilizar os conceitos de derivada de decrescimento, crescimento, valores de máximo, valores de mínimo e pontos de inflexão para esboçar uma primitiva de .
E teremos que lembrar que quando:
Olhando para o gráfico dado, podemos analisar o que está acontecendo com a primitiva da nossa função com base, nas informações sobre sua derivada.
Vem que te mostro como.
E aí? Bora lá?? 😉
Passo 2
Usando uma calculadora, podemos mostrar o gráfico de no intervalo dado:
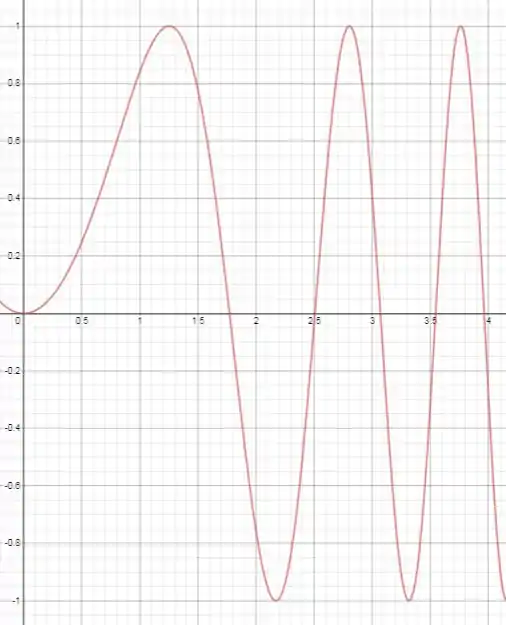
Se é a antiderivada de , então
e estamos olhando para o gráfico da inclinação de . Com isso, conseguimos estimar como se comporta a função .
Passo 3
Sabemos que:
E vemos que o gráfico começa em com inclinação zero.
Depois a inclinação aumenta até 1 em e volta a diminuir até zero em .
Como a inclinação é zero, temos aí um ponto máximo.
Depois a inclinação é negativa e a curva é decrescente até o ponto mínimo em .
Volta a crescer, tem um máximo em , depois desce e tem um mínimo em e finalmente volta a crescer e tem outro máximo em .
Um gráfico estimado da função é mostrado:
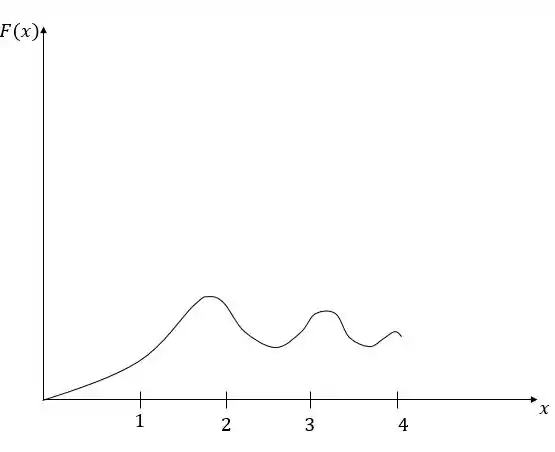
E prontinho.
Resposta
