Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 72
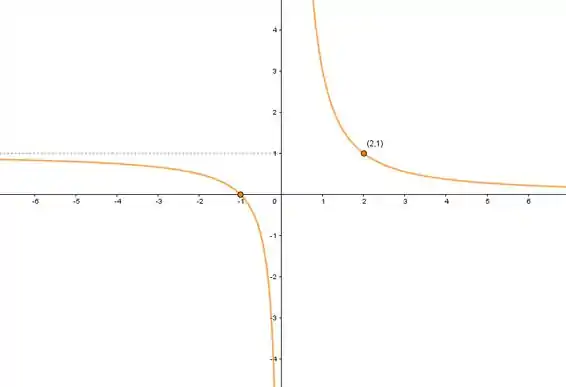
Trace o gráfico de uma função que satisfaça as condições dadas.
, , , e
Passo 1
O primeiro passo é olhar o tipo de resposta que o limite apresenta, ou seja, se zero, um número ou . Com isso, nós podemos ver qual tipo de função se encaixa melhor para cada caso.
Na questão temos que, e , isso significa teremos que avaliar cada um desses limites.
Quando observamos uma divisão de polinômios de mesmo grau, onde o grau do polinômio de baixo fosse maior que grau o do polinômio de cima seria uma boa, já que nesses casos, quando o limite dará . Veja no exemplo abaixo:
Já quando parece que uma divisão de polinômios de mesmo grau , seria uma boa, já que nesses casos, quando o limite dará . Veja no exemplo abaixo:
Isso significa que terá que ser definida de duas maneiras.
Passo 2
O segundo passo é perceber que o limite dessa função assume valores diferentes quando e quando ,ou seja, quando os valores de vão diminuindo, já quando esses valores vão aumentando. Então para simplificar as coisas vamos separar o problema em duas partes, ou seja, vamos imaginar a cara da função quando e quando .
Lembrando que quando, , deve uma divisão de polinômios de mesmo grau, onde o grau do polinômio de baixo fosse maior que grau o do polinômio de cima pelo que vimos no Passo 1, sendo assim a cara de pode ser da forma:
O que é TOP pois,
E,
Além disso,
Agora, quando , deve uma divisão de polinômios de mesmo grau, onde o grau do polinômio de baixo fosse menor que grau o do polinômio de cima pelo que vimos no Passo 1, sendo assim a cara de pode ser da forma:
O que é TOP pois,
E,
Além disso,
E portanto,
Resposta
