Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 64b

A B C é um triângulo retângulo com o ângulo reto em C . Os lados opostos aos ângulos A ,   B e C são a ,   b e c , respectivamente.

Expresse s e n A em função de b e c .

Passo 1

E aí, galera! Vou te mostrar como fica o esboço desse desenho:

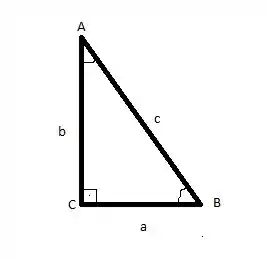
Pra esse problema, precisamos lembrar que:

seno: s e n x = c a t e t o   o p o s t o h i p o t e n u s a

fórmula de Pitágoras: h i p o t e n u s a 2 = ( c a t e t o   o p o s t o ) 2 + ( c a t e t o   a d j a c e n t e ) 2

Passo 2

Aqui, vamos ver o que a gente vai usar a partir do que ele quer. Ele quer que envolva o ângulo A, então a relação trigonométrica vai ser usada a partir dele. Então, em relação a A, b é o cateto adjacente, a é o cateto oposto e c é a hipotenusa. Como ele quer s e n A em função de c (hipotenusa) e b (cateto adjacente), vamos aplicar o seno e depois fazer aparecer o b .

s e n x = c a t e t o   o p o s t o h i p o t e n u s a → s e n A = a c

Beleza, mas a gente quer que apareça o b , né? Então, aquele a dali tem que sumir. Pra isso, precisamos de uma relação que envolva a e b : a fórmula de Pitágoras.

h i p o t e n u s a 2 = ( c a t e t o   o p o s t o ) 2 + ( c a t e t o   a d j a c e n t e ) 2 → c 2 = a 2 + b 2 → a 2 = c 2 - b 2 → a = c 2 - b 2

Substituindo na equação do seno:

s e n A = a c → s e n A = c 2 - b 2 c

Resposta

s e n A = c 2 - b 2 c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para f x = A sen ⁡ 2 π B x - C + D , identifique A, B, C e D para as funções seno dos Exercícios 65-68 e esboce seus gráficos.65. y = 2 sen ⁡ ( x + π ) - 1
Para f x = A sen ⁡ 2 π B x - C + D , identifique A, B, C e D para as funções seno dos Exercícios 65-68 e esboce seus gráficos.67. y = - 2 π sen ⁡ π 2 t + 1 π
63. Um trângulo possui lado c = 2 e ângulos A = π / 4 e B = π / 3 . Determine o comprimento a do lado oposto de A .
61. Lei dos Senos A lei dos senos diz que se a, b e c são os lados opostos aos ângulos A, B e C em um triângulo, então sen ⁡ A a = sen ⁡ B b = sen ⁡ C c Use as figuras a seguir e a identidade sen ⁡ (
Nos Exercícios 69-72, você explorara gráficamene a função seno geral f x = A sen ⁡ 2 π B x - C + D , Enquanto altera os valores das constantes A, B, C e D. Utilize um CAS ou software de gráfico para s