61. Lei dos Senos A lei dos senos diz que se a, b e c são os lados opostos aos ângulos A, B e C em um triângulo, então sen ⁡ A a = sen ⁡ B b = sen ⁡ C c Use as figuras a seguir e a identidade sen ⁡ ( π - θ ) = sen ⁡ θ , se necessário, para deduzir a lei.

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 61

61. Lei dos Senos A lei dos senos diz que se a, b e c são os lados opostos aos ângulos A, B e C em um triângulo, então

Use as figuras a seguir e a identidade , se necessário, para deduzir a lei.

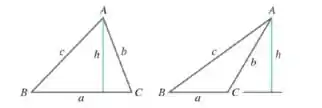
Passo 1

Para conseguirmos deduzir a Lei dos senos, precisamos encontrar relações trigonométricas, usando o seno, nos triângulos. Depois podemos observar o que devemos fazer com essas relações, até que a gente encontre a Lei.

Podemos calcular o seno de B e de C da primeira imagem facilmente:

Na segunda imagem:

Já o seno de podemos calcular com a identidade fornecida no enunciado, pois da imagem a gente sabe que

logo

Então, não importa o tipo de triângulo, essas relações sempre são válidas:

Isolando o e igualando as equações temos:

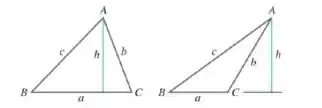
Passo 2

Se a reta, de tamanho , for traçada perpendicularmente ao lado de tamanho ou , chegaremos analogamente as relações:

, se a reta for perpendicular ao lado

Igualando as equações chegamos na Lei dos senos:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da

Use a periodicidade das funções tangente e cotangente, bem como os valores do t g t , e c o t g ( t ) , quando 0 ≤ tπ , para determinar o valor exato da função t g - 5 6 π .