Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 63
63. Um trângulo possui lado e ângulos e . Determine o comprimento do lado oposto de .
Passo 1
Com as informações dadas não conseguimos encontrar o comprimento diretamente, então vamos usar a Lei dos senos e a Lei dos cossenos.
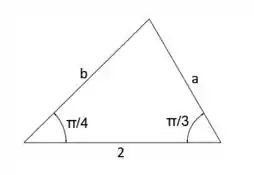
Primeiro vamos usar a Lei dos cossenos:
Passo 2
Agora precisamos usar a Lei dos senos:
Passo 3
Isolando para substituir na equação :
Substituindo
Como :
Resposta
Exercícios de Livros Relacionados
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da
Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ( t ) , s e c ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da