Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 26
Use uma calculadora para avaliar a integral de linha correta até quatro casas decimais.
onde tem equações paramétricas .
Passo 1
Faaaaala galerinha, tudo bem!? Vamos nessa!!!
Temos que determinar o valor em até quatro casas decimais utilizando calculadora da seguinte integral de linha:
Onde, tem equações paramétricas
E agora?
A maior dificuldade dessa questão, consiste em montar a integral na forma parametrizada, certo? Porque vamos utilizar calculadora para resolver.
Logo, você terá que substituir , e pelas parametrizações, e lembre-se que tem uma forma parametrizada também. Que é:
Assim, é só você montar a integral e utilizar uma calculadora de sua preferência que resolva integrais. Sugiro utilizar a calculadora online WolframAlpha.
Bora lá!!
Passo 2
Nosso objetivo é parametrizar a seguinte integral:
Sabemos que:
E que é:
Agora vamos encontrar . E para isso é só fazer as derivadas e substituir na formula acima.
Fazendo isso, vamos ter:
Agora vamos montar a integral. Substituindo os valores vamos ter:
Simplificando um pouco, temos:
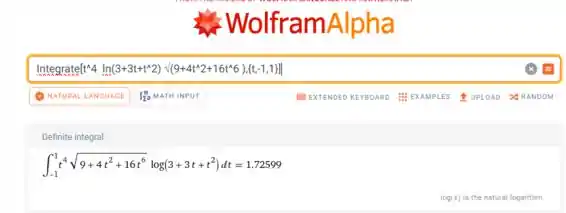
Utilizando o WolframAlpha com o input:
Integrate[t^4 ln(3+3t+t^2) √(9+4t^2+16t^6 ),{t,-1,1}]
Obtemos como resposta:
