Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.2 - Ex. 48
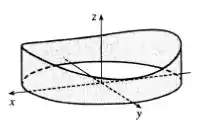
A base de uma cerca circular de raio é dada por A altura da cerca na posição é dada pela função , portanto a altura varia a . Suponha que de tinta permita pintar . Faça um esboço da cerca e determine quanto de tinta você precisará para pintar os dois lados da cerca.
Passo 1
E aiii galera, tudo bem? Vamos começar.
Essa questão tem bastante informação, então quero que você preste atenção e análise com calma.
As equações paramétricas a seguir descrevem a base circular de uma cerca que tem de raio:
A altura dessa cerca, que varia entre a é descrita pela seguinte equação:
Supondo que de tinta permita pintar . Primeiro devemos fazer um esboço da cerca e depois determinar quanto de tinta precisaremos para pintar os dois lados da cerca.
Fica tranquilo, vamos montar uma estratégia de resolução juntos, beleza?
Pra fazer o esboço, vamos primeiro parametrizar a expressão , com as parametrizações dadas. Fazendo isso você vai ter uma função:
Assim, você pode utilizar um software como o Geogebra para plotar esse gráfico, pois fazer a mão é meio complicado.
Para determinar o quanto de tinta precisamos, vamos ter que calcular a área dessa cerca. Para isso devemos calcular:
Porém, repare que multiplicamos por para obter a área dos dois lados da cerca. Achando a área, você aplicar uma regra de três e determinar quantos litros de tinta são necessário.
Quando temos esse tipo de função, que é um escalar, nosso é escrito como:
Agora está molezinha ein! Vamos nessa!
Passo 2
Vamos começar determinando um esboço dessa cerca.
O enunciado nos forneceu a parametrização da base da cerca, e também a expressão da altura da cerca.
A base é:
A altura é:
Se parametrizarmos a altura, vamos ter uma expressão que escreve a cerca em relação a base. Que vai ser:
E com a ajuda de uma calculadora gráfica temos o seguinte esboço:
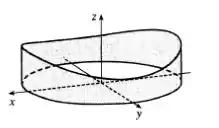
Agora vamos calcular a área dessa cerca? Beleza!
Passo 3
A área vai ser:
Já temos h(x,y) parametrizado do passo anterior, que é:
com,
Agora precisamos determinar , que é:
Fazendo as derivadas da parametrização e aplicando da raiz, vamos ter:
Pronto! Agora é só colocar na integral tudo isso!
Passo 4
Vamos montar a integral.
Mas antes vamos simplificar mais nossa expressão :
Vamos substituir pelas relações trigonométricas a seguir:
Ficando assim:
Assim, ficamos com:
Viu só, isso vai facilitar muito nossa vida na hora de integrar.
Lembrando também que:
Substituindo na integral temos que:
Passo 5
Agora vamos resolver a integral:
Podemos separar em duas integrais:
Repare, que precisamos fazer uma substituição na segunda integral do tipo:
Substituindo, temos:
Integrando e voltando a variável , vamos ter:
Aplicando os limites temos:
Assim, temos que a soma da área interna e externa da cerca vale:
Passo 6
Agora vamos utilizar da regra de três para determinar quantos litros de tintas são necessários para pintar a cerca por dentro e por fora.
Sabendo que os dois lados da cerca vão ter num total de de área e que pinta , com a regra de três temos:
Multiplicando cruzado temos:
Então serão necessários aproximadamente de tinta para pintar a parte interna e externa da cerca.
Resposta
