Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 39
Use um computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela retangular até conseguir uma boa visão da superfície.
Passo 1
Bom, pessoal. Vamos usar a equação do enunciado pra traçar a superfície tridimensional de alguns pontos de vista.
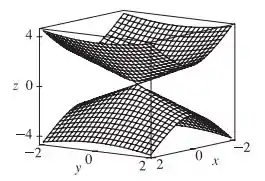
Show! Podemos ver que isso é um cone elíptico!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
1 . Determine o plano tangente à superfície dada, no ponto dado. σ( u ,v )=( u ,v ,u 2+v 2 ) ,n op o n t oσ( 1 ,1 ) . σ( u ,v )=( cos u , sin u , v ) ,n op o n t oσ( π 2 ,1 ) . σ( u ,v )=( 2 u+v ,
1 . Determine o plano tangente à superfície dada, no ponto dado. σ( u ,v )=( u ,v ,u 2+v 2 ) ,n op o n t oσ( 1 ,1 ) . σ( u ,v )=( cos u , sin u , v ) ,n op o n t oσ( π 2 ,1 ) . σ( u ,v )=( 2 u+v ,
1 . Determine o plano tangente à superfície dada, no ponto dado. σ( u ,v )=( u ,v ,u 2+v 2 ) ,n op o n t oσ( 1 ,1 ) . σ( u ,v )=( cos u , sin u , v ) ,n op o n t oσ( π 2 ,1 ) . σ( u ,v )=( 2 u+v ,
1 . Determine o plano tangente à superfície dada, no ponto dado. σ( u ,v )=( u ,v ,u 2+v 2 ) ,n op o n t oσ( 1 ,1 ) . σ( u ,v )=( cos u , sin u , v ) ,n op o n t oσ( π 2 ,1 ) . σ( u ,v )=( 2 u+v ,
Descreva e esboce a superfície. y 2 + 4 z 2 = 4