Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 41
Esboce a região delimitada pelas superfícies e para .
Passo 1
Beleza, pessoal? Primeiro, vamos identificar que superfícies são essas? Em a equação
representaria uma circunferência, né mesmo? Mas como estamos falando de , isso representa um cilindro circular!
Passo 2
Show! Agora, vamos fazer uma pequena modificação na outra equação:
Veja que isso é a equação de um cone elíptico (mais especificamente, cone circular). Mas a equação original nos diz que (pois a raiz quadrada é sempre não negativa), então ela representa apenas a parte superior do cone.
Passo 3
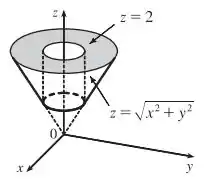
Se fizermos o esboço das duas superfícies, vamos ver que a região delimitada pelas duas é a que está em cinza, a seguir:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use cortes para esboçar e identificar as superfícies. 4 x 2 - 16 y 2 + z 2 = 16
Use cortes para esboçar e identificar as superfícies. 9 x 2 - y 2 + z 2 = 0
Use cortes para esboçar e identificar as superfícies. x = y 2 - z 2
Use cortes para esboçar e identificar as superfícies. y = z 2 - x 2
Use cortes para esboçar e identificar as superfícies. x 2 = y 2 + 4 z 2