Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.6 - Ex. 17
Use cortes para esboçar e identificar as superfícies.
Passo 1
Beleza, galera? Primeiro, vamos fazer os cortes, igualando cada variável a uma constante arbitrária . Vamos começar com :
- :
- :
- :
Então esse corte é uma elipse, quando . Isso equivale a:
Passo 2
Continuando:
Ou seja, o corte é uma elipse, quando , isto é,
Novamente, temos uma elipse quando , ou seja, como já vimos,
Passo 2
Show! Juntando todas essas informações, podemos esboçar a superfície:
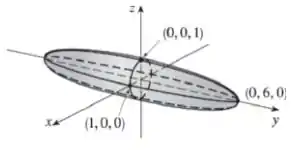
Veja que isso é um elipsoide, beleza?
Resposta
Elipsoide
Exercícios de Livros Relacionados
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. x 2 + 4 y 2 + z 2 = 4
Determine o traço da superfície dada nos planos x = k ,y = k , z = k . Identifique a superfície e faça um esboço dela. z = x 2 - y 2
Use o computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela de inspeção até conseguir uma boa visão da superfície.38- 8 x
Use o computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela de inspeção até conseguir uma boa visão da superfície.40- z =
Use o computador com um programa que trace superfícies tridimensionais. Experimente diversos pontos de vista e diversos tamanhos de janela de inspeção até conseguir uma boa visão da superfície.37- z =