Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.2 - Ex. 1
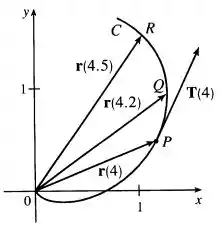
A figura mostra uma curva dada pela função vetorial .
(a) Desenhe os vetores e .
(b) Esboce os vetores
(c) Escreva a expressão para e para seu vetor tangente unitário .
(d) Desenhe o vetor .
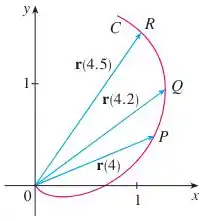
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico que mostra uma curva com os pontos e com seus respectivos vetores:
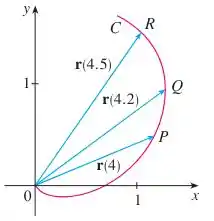
Primeiramente queremos desenhar os vetores e .
Para isso, basta sabermos que a seta partirá do subtraendo em direção ao minuendo.
Em seguida, queremos esboçar os seguintes vetores:
Para isso, basta fazermos como a letra a). No entanto, a nossa seta aumentará o tamanho por conta do número que está dividindo ser menor que zero.
Na letra c) queremos encontrar a expressão para e para seu vetor tangente unitário .
Para isso, vamos aplicar a definição para calcular essa derivada e, em seguida, vamos encontrar seu vetor tangente unitário utilizando a seguinte relação:
Por fim, na letra d), queremos esboçar o vetor .
Passo 2
(a) Bom... Sabendo que a seta partirá do subtraendo em direção ao minuendo, vamos ter os seguintes vetores:
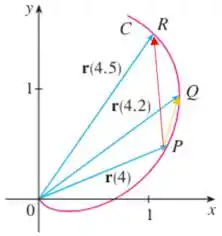
Onde a seta vermelha é o vetor e a seta amarela é o vetor .
Passo 3
(b) Também na figura, vamos esboçar os vetores correspondentes. Repara o seguinte:
Ou seja, vai ser aquele vetor da seta vermelha, mas aumentado em duas vezes.
Da mesma forma, teremos:
Ou seja, vai ser aquele vetor da seta amarela, mas aumentado em cinco vezes.
Em suma, esses vetores terão a mesma direção e sentido dos vetores do item anterior, o que muda é apenas a magnitude, o tamanho:
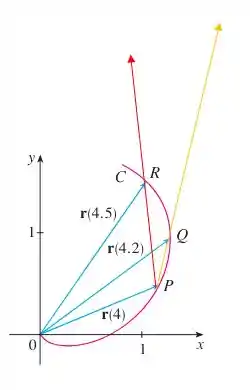
Onde a seta vermelha é o vetor e a seta amarela é o vetor .
Passo 4
(c) Por definição, temos:
Aplicando , teremos:
No passo 1, vimos que:
Para , teremos:
Passo 5
(d) Galera, deve ser um vetor unitário que tem a mesma direção e sentido de , ou seja, deve ser paralelo à reta tangente à curva em .
O desenho vai ficar assim então:
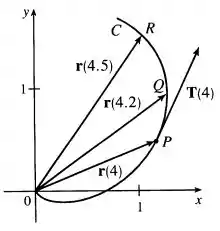
Resposta
(a)
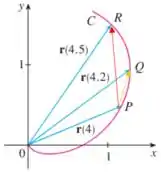
(b)
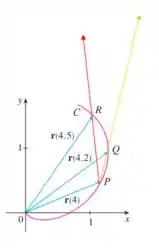
(c)
(d)
