Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 71
Use a desigualdade para estimar se para e .
Passo 1
Utilizando a desigualdade apresentada queremos uma estimativa para , com a função e a condição inicial dada.
Passo 2
Para analisarmos o comportamento da função dentro do intervalo, vamos observar a segunda derivada que é
Plotando o gráfico de dentro do intervalo temos
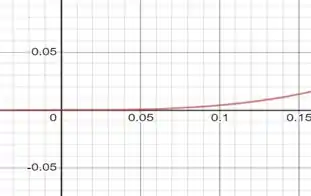
a função está decrescendo.
Passo 3
Como temos decrescendo nesse intervalo nós podemos fazer estimativas para com os valores extremos do intervalo. Assim,
Resposta
Exercícios de Livros Relacionados
Foram necessários 14 s para que um termômetro de mercúrio subisse de -19º C º para 100º C º após ser retirado do congelador e colocado em água fervente. Demonstre que em algum ponto a coluna de mercúr
A média aritmética de dois números a e b é a +b 2 . Mostre que o valor de c na conclusão do teorema do valor médio para f x = x 2 em qualquer intervalo [a ,b ] é c=a+b2 .
O Exercício fornece a aceleração a = d 2 s d t 2 , a velocidade inicial e a posição inicial de um corpo que se desloca ao longo de uma reta coordenada. Determine a posição do corpo no instante t para
A média geométrica de dois números positivos a e b é o número a b . Demonstre que o valor de c na conclusão do teorema do valor médio para f x = 1 x em um intervalo de números positivos [a, b] é c = a
O Exercício fornece a aceleração a = d 2 s d t 2 , a velocidade inicial e a posição inicial de um corpo que se desloca ao longo de uma reta coordenada. Determine a posição do corpo no instante t para