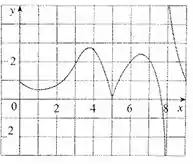
Use o gráfico dado de f para encontrar o seguinte:O maior intervalo aberto no qual f é crescenteO maior intervalo aberto no qual f é decrescenteO maior intervalo aberto no qual f é côncava para cimaO maior intervalo aberto no qual f é côncava para baixoAs coordenadas do ponto de inflexão.

Enunciado

Oiee, vamos resolver essa questão?

A teoria da concavidade refere-se ao comportamento de uma função em relação às suas curvaturas, e está relacionada com a segunda derivada da função.

1. Concavidade para cima (Côncava para cima):

- Uma função é côncava para cima em um intervalo se sua derivada segunda é positiva nesse intervalo.

- Graficamente, isso significa que a curva de fica "para cima", como a forma de uma tigela ou um sorriso.

- Intuitivamente, se você desenhar uma linha tangente em qualquer ponto desse intervalo, a função estará acima da tangente.

2. Concavidade para baixo (Côncava para baixo):

- Uma função é côncava para baixo em um intervalo se sua derivada segunda é negativa nesse intervalo.

- Graficamente, isso significa que a curva de fica "para baixo", como a forma de um arco ou uma carranca.

- Intuitivamente, se você desenhar uma linha tangente em qualquer ponto desse intervalo, a função estará abaixo da tangente.

Ponto de Inflexão

- Um ponto de inflexão é um ponto onde a função muda sua concavidade, isto é, de côncava para cima para côncava para baixo, ou vice-versa.

- Matematicamente, um ponto é um ponto de inflexão se a segunda derivada muda de sinal (de positiva para negativa ou de negativa para positiva) em

Para acharmos o maior intervalo no qual nossa função é crescente vamos olhar em quais ela é crescente e escolher o maior. Nossa função será crescente enquanto os valores de continuarem crescendo. Analisando o gráfico temos os seguintes intervalos:

Logo, o maior intervalo será .

Para acharmos o maior intervalo no qual nossa função é decrescente vamos olhar em quais ela é crescente e escolher o maior. Nossa função será decrescente enquanto os valores de forem diminuindo. Analisando o gráfico temos os seguintes intervalos:

,, e

Como só temos apenas um intervalo, ele será o maior. Assim, o maior intervalo no qual é decrescente será

A função será côncava para cima quando a curva fizer um vale. Analisando o gráfico dado, vemos que ela será côncava pra cima nos seguintes intervalos:

Como os intervalos possuem o mesmo tamanho:

A função será côncava para baixo quando a curva fizer um morro. Analisando o gráfico dado, vemos que ela ser�� côncava pra baixo nos seguintes intervalos:

Logo, o maior intervalo será

Os pontos de inflexão são os pontos nos quais as funções deixa de ser crescente para ser decrescente e vice versa. Assim, teremos os seguintes:

Vide a explicação.