Se , mostre que 0 é um número crítico de , mas que não é um extremo relativo. A origem é um ponto de inflexão do gráfico de Prove sua resposta,
Passo 1
Para começar precisamos determinar os pontos críticos da função. Os números críticos são caracterizados pelos valores de x que permitam ou para os quais não exista. Então, o primeiro passo é calcularmos a derivada primeira:
A função é contínua para todos os valores de x. Sendo assim, precisamos somente de igualar a função a 0:
Comprovamos que 0 é um ponto crítico da função. O próximo passo é avaliar se este ponto é um extremo relativo.
Passo 2
Para determinar se tem um extremo relativo nesse ponto, aplicamos o teste da derivada primeira:
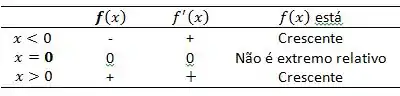
Como a função continua a crescer, 0 não é um extremo relativo.
Passo 3
Para descobrir os pontos de inflexão do gráfico, precisamos da derivada segunda:
Uma vez descoberta a derivada segunda, os pontos de inflexão são caracterizados por :
Neste caso, a função será igual a 0 no ponto Mas para que um ponto seja classificado como ponto de inflexão a concavidade deve mudar de direção em valores maiores e menores que este.
Analisando a mudança de direção da concavidade:

Sendo assim, é um ponto de inflexão.
Desenhando o gráfico da função para comprovarmos o que foi visto:
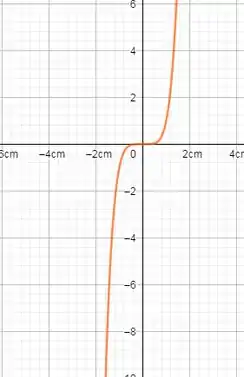
Resposta
Ei, a resposta está no passo a passo :)