Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata
Passo 1
Se esboçarmos o gráfico de , ficamos com
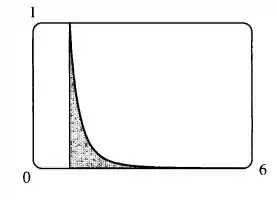
Podemos estimar a área
Passo 2
Como a gente faz pra encontrar a área embaixo de uma curva? A gente integra não é mesmo? Então é só a gente integrar a função no intervalo dado
Resposta
Estimando:
Calculando: