Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 51
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata
Passo 1
Fala aí, tudo belezinha como você?
Bom, essa questão dá pra gente a curva
E peder pra gente usar um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada e a seguir, achar a área exata.
Bom, faremos exatamente o que ele pediu. Primeiro vamos traçar o gráfico da curva no intervalo dado e estivar a área abaixo dele de acordo com imagem formada.
Depois, como precisamos da área exata, usaremos a integração para nos ajudar já que a integral pode ser entendida como a área sob o gráfico da função.
Assim, faremos:
Vamos nessa!
Passo 2
Podemos começar esboçando o gráfico de , e ficamos com
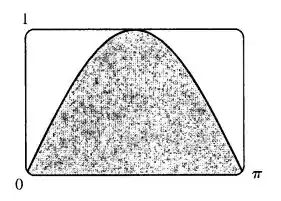
Podemos estimar a área
Agora vamos calcular essa área com exatidão.
Passo 3
Como a gente faz pra encontrar a área embaixo de uma curva? A gente integra, não é mesmo?
Então é só a gente integrar a função no intervalo dado
Lembrando que a integral do seno é igual a menos o cosseno, teremos:
Como essa é uma integração definida, vamos substituir os limites de integração na função dada. Assim:
O que nos dará:
Assim, temos a área exata abaixo da curva do seno no integrvalo dado.
Resposta
Estimando:
Calculando: