Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 49
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. Encontre a seguir a área exata.
Passo 1
Oi, galera ☺️!
Nesse exercício, precisamos estimar e calcular a área que fica abaixo da curva
Para estimar a área, vamos usar uma ferramenta gráfica para eboçar o gráfico de e obter essa estimativa a partir da área de retângulos.
Agora, para encontrar a área exata, vamos lembrar que a área abaixo da curva é dada por uma integral definida. De fato, calcular a área abaixo da curva é equivalente a calcular a integral
Pra facilitar nosso trabalho, vamos relembrar da Parte do Teorema Fundamental do Cálculo:
- Se é uma primitiva de , ou seja, se , então
- Temos 14 retângulos inteiros.
- 8 retângulos para entre 3 e 27, e entre 0 e 1.
- 6 retângulos para entre 9 e 27, e entre 1 e 2.
- Para entre 0 e 3, vamos contar mais retângulo (temos quase um inteiro para entre 0 e 1, e um pedacinho de outro para entre 0 e 2).
- Para entre 3 e 6 e entre 1 e 2 temos mais da metade de um retângulo.
- Para entre 6 e 9 e entre 1 e 3 parece que temos quase mais retângulo (somando os dois pedaços).
- Para entre 9 e 27 e entre 2 e 3, temos 6 pedaços de retângulo, se juntarmos os maiores com os menores parece que teremos mais de 3 retângulos completos, né?
Observe que no nosso caso , e Então, precisamos apenas encontrar uma primitiva da função e fazer as contas necessárias, beleza?
Para encontrar uma primitiva, usamos a Regra da Potência: Para , uma primitiva da função é
Pronto! Temos tudo o que precisamos pra fazer essa questão. Bora lá resolver 🤓?
Passo 2
Começamos esboçando o gráfico, beleza?
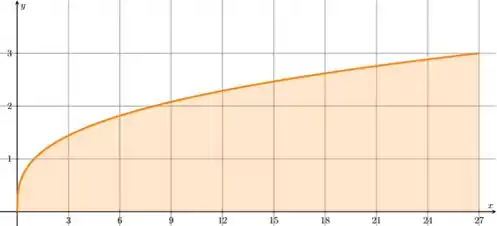
Note que a escala dos eixos é diferente, cada quadradinho no gráfico na verdade é um retângulo de área . Vamos contar quantos retângulos temos?
Isso quer dizer que temos mais de retângulos, vamos arredondar para 20 então!
Como cada retângulo tem área , nossa estimativa para a área da região que fica abaixo da curva é
Passo 2
Para calcular a área exata usando a Parte do Teorema Fundamental, vamos começar encontrando uma primitiva da função
Para facilitar, reescrevemos a função da seguinte maneira:
Agora, aplicando a Regra da Potência, temos que
é uma primitiva da função .
Logo, pela Parte do Teorema Fundamental do Cálculo, vale que
Mas, como temos que
e
então temos que o valor da integral é
Escrevendo como número decimal
que é bem próximo do valor que estimamos no Passo anterior, né 😁?
Resposta
A área estimada a partir do gráfico foi
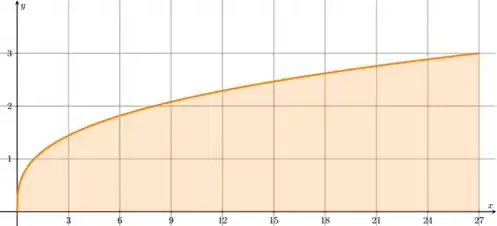
A área exata calculada foi