Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 7

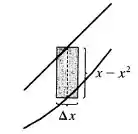
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximante típico e coloque sua altura e largura. Então, calcule a área da região.

Passo 1

Fala aí! tudo certinho?

Bom galera, nesse exercício iremos calcular a área da região delimitada entre as curvas

Pra isso, utilizamos a integração, iremos esboçar a região e desenhar um retângulo aproximadamente. Para isso, iremos utilizar a seguinte definição de área

Veja só!

Passo 2

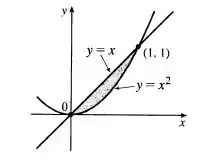
Primeiramente, devemos encontrar a interseção das curvas. Para isso, iremos igualar as equações

Dessa forma, ou ou . Podemos esboçar a curva

Tranquilo até aqui?

Passo 3

Utilizando a definição do passo , temos

Calculando a integral e aplicando os limites de integração...

E aí! tudo certinho? Responde Aí!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A área da região que está à direita do eixo y e à esquerda da parábola x = 2 y - y 2 (a região sombreada na figura) é dada pela integral ∫ 0 2 2 y - y 2d y . (Gire sua cabeça no sentido horário e imag

Use um gráfico para estimar a intersecção com o eixo x da curva y = x + x 2 - x 4 . A seguir, use essa informação para estimar a área da região que se situa sob a curva e acima do eixo x .

Use um gráfico para estimar a intersecção com o eixo x da curva y = 2 x + 3 x 4 - 2 x 6 . A seguir, use essa informação para estimar a área da região que se situa sob a curva e acima do eixo x .

As fronteiras da região sombreada são o eixo y , a reta y = 1 e a curva y = x 4 . Ache a área dessa região escrevendo x como uma função de y e integrando em relação a y (como no Exercício 4 9 ).

Os economistas usam uma distribuição acumulada chamada curva de Lorenz para descrever a distribuição de renda entre as famílias em um dado país. Tipicamente, uma curva de Lorenz é definida no interval