Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.1 - Ex. 37

Use um gráfico para encontrar as coordenadas aproximadas x dos pontos de intersecção das curvas dadas. A seguir, encontre a área aproximada da região limitada pelas curvas

y = 3 x 2 - 2 x ,     y = x 3 - 3 x + 4

Passo 1

Bom galera, nesse exercício queremos encontrar as coordenadas aproximadas dos pontos de interseção das curvas dadas e calcular a área da região limitada pelas curvas. Para isso, utilizaremos os conceitos de área entre curvas e esboçaremos o gráfico das funções.

Passo 2

Esboçando a curva, temos

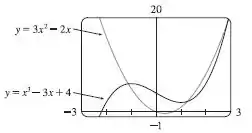
Passo 3

Podemos escrever a seguinte integral

A = ∫ a b x 3 - 3 x + 4 - 3 x 2 - 2 x d x + ∫ b c 3 x 2 - 2 x - x 3 - 3 x + 4 d x

Onde a = - 1.11 , b = 1.25 e c = 2.86 . As curvas se interceptam em a , b e c . Resolvendo a integral, temos

A = x 4 4 - x 3 - x 2 2 + 4 x a b + - x 4 4 + x 3 + x 2 2 - 4 x b c = 8.38

Resposta

As curvas se interceptam em - 1.11 , 1.25 e 2.86 .   A = 8.38 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas