Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.1 - Ex. 32

Calcule a integral e interprete-a como a área de uma região. Esboce a região.

∫ 0 4 x + 2 - x d x

Passo 1

Bom galera, nesse exercício iremos calcular a integral apresentada e interpretar como a área de uma região. Dessa forma, após calcular a integral iremos esboçar a região em questão.

Passo 2

Primeiramente iremos simplificar a integral devido ao módulo da seguinte maneira

∫ 0 4 x + 2 - x d x = ∫ 0 4 x + 2 - x d x + ∫ 0 4 x - x + 2 d x

Dessa forma, temos duas integrais elementares que podem ser resolvidas utilizando o conceito de antiderivada

∫ 0 4 x + 2 - x d x + ∫ 0 4 x - x + 2 d x = 2 3 x + 2 3 / 2 - x 2 2 0 4 + x 2 2 - 2 3 x + 2 3 / 2 0 4

Passo 3

Aplicando os limites de integração, temos

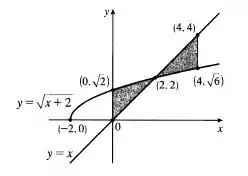
2 3 x + 2 3 / 2 - x 2 2 0 4 + x 2 2 - 2 3 x + 2 3 / 2 0 4 = 2 3 4 + 2 3 / 2 - 4 2 2 - 2 3 0 + 2 3 / 2 - 0 2 2 + 4 2 2 - 2 3 4 + 2 3 / 2 - 0 2 2 - 2 3 0 + 2 3 / 2 = 44 3 - 4 6 - 4 3 2

Esboçando a região graficamente, temos

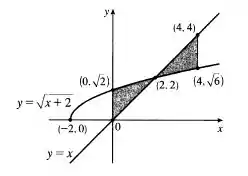
Resposta

∫ 0 4 x + 2 - x d x = 44 3 - 4 6 - 4 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas