Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 8.3 - Ex. 26

Esboce a região delimitada pelas curvas, e visualmente estime a localização do centroide. A seguir, calcule as coordenadas exatas do centroide.

3 x + 2 y = 6 ,   y = 0 ,   x = 0

Passo 1

Bom galera, nessa questão queremos encontrar o centroide delimitado pelas curvas. Para isso, iremos esboçar graficamente e iremos calcular as coordenadas exatas do centroide utilizando as definições do centroide.

Passo 2

Por definição, temos que

x - = 1 A ∫ x 1 x 2 x f x d x

y - = 1 2 A ∫ x 1 x 2 f x 2 d x

Dessa forma, temos que

A = ∫ 0 2 3 - 3 2 x d x = 3 x - 3 4 x 2 0 2 = 3

Passo 3

Calculando utilizando as definições do passo anterior, temos

x - = 1 3 ∫ 0 2 x 3 - 3 2 x d x = 1 3 3 2 x 2 - 1 2 x 3 0 2 = 2 3

y - = 1 6 ∫ 0 2 3 - 3 2 x 2 d x = 1 6 9 x - 9 2 x 2 + 3 4 x 3 0 2 = 1

Graficamente

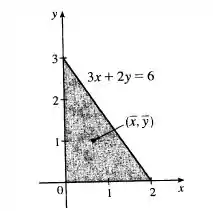
Resposta

x - ,   y - = 2 3 , 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o volume do sólido obtido pela rotação de A em torno da reta y = 2 .
Calcule o volume do sólido obtido pela rotação do circulo x 2 + y 2 ≤ 1 em torno da reta x + y = 2
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 2 1 - x d x
Calcule a integral, interpretando-a em termo de áreas. ∫ 0 9 1 3 x - 2 d x
Determine o centro de massa da região A dada por 1 ≤ x 2 + y 2 ≤ 4 , x ≥ 0 e y ≥ 0 .