Use um gráfico para encontrar os valores aproximados das coordenadas dos pontos de intersecção das curvas dadas. A seguir, encontre (aproximadamente) o volume do sólido obtido pela rotação em torno do eixo da região limitada por essas curvas.
Passo 1
Fala aí, pessoal! 😉

Nesse problema temos duas curvas e e nosso objetivo é encontrar os pontos de intersecção entre elas e o volume do solido formado pela rotação da area formada...
Tem ideia de como fazemos isso? 😐
Para determinar os pontos em que as curvas se tocam, podemos igualas as equações como .
Já para determinar o volume do solido a partir de sua revolução, usamos o método dos discos...
Veja só! 😁
Passo 2
O gráfico formado é o seguinte:
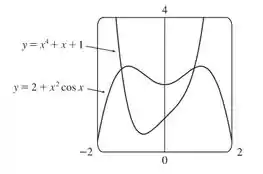
Fazendo , temos
A duas funções se interceptam nos pontos e .
Tranquilo até aqui? 😉
Passo 3
Agora calculamos o volume da supoerficie de revolução pelo método dos discos, ou seja
No caso, que é a curva maior e que é a curva menor
Calculando essa integral, temos
E aí! O que achou? Responde Aí! 😊
