Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 38
Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas.
Passo 1
Vamos analisar esse problema. Bom, precisamos entender como cada gráfico se comporta, certo?
Então, o gráfico de uma polinomial é uma curva, né não? Então já sabemos que será uma e para cima porque o valor do coeficiente angular é positivo
Agora, a função é uma função racional. Com isso, podemos ter uma noção do nosso graficozinho, que será assim:
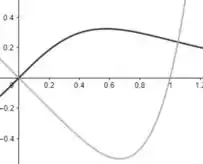
Por ele, identificamos a região de interseção onde . Dizemos que e , por que não sabemos no momento quanto vale o outro ponto então chamamos de . Pelo gráfico, percebemos que o valor de é mais ou menos .
Assim, podemos calcular a área!!
Passo 2
Calculando a área, temos
Vamos resolvê-la!!
Aplicamos o método da substituição para a primeira função,
Substituindo na integral,
Agora podemos resolver as integrais:
Colocando o valor de u: