Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.1 - Ex. 36

Use um gráfico para encontrar os valores aproximados das coordenadas x dos pontos de intersecção das curvas indicadas. A seguir, encontre a área aproximada da região delimitada pelas curvas.

y = e x ,   y = 2 - x 2

Passo 1

Primeiro, precisamos entender como cada função se comporta num gráfico. Sabemos que a exponencial é uma curva que nunca toca nos eixos. Já a função y = 2 - x 2 será uma curva para baixo porque o coeficiente angular é menor que zero.

Assim, o nosso gráfico será:

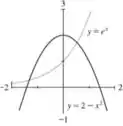
A partir dele podemos encontrar os nossos pontos de interseção. Dizemos que x = a ≅ - 1,32 e x = b ≅ 0,54 .

Agora podemos calcular a nossa área !!

Passo 2

Como 2 - x 2 > e x , então

A = ∫ - 1,32 0 , 5 4 ( 2 - x 2 ) - e x d x

Resolvendo a integral normalmente...

A = 2 x - x 3 3 - e x - 1,32 0,54

A = 2 0,54 - 0,54 3 3 - e 0,54 - 2 - 1,32 - - 1,32 3 3 - e - 1,32

A = 2 0,54 - 0,54 3 3 - e 0,54 - 2 - 1,32 - - 1,32 3 3 - e - 1,32

A = - 0,689 - - 2 , 140

A = - 0,689 - - 2,140

A = 1,45

Resposta

A = 1,4 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as áreas totais das regiões sombreadas
Determine as áreas totais das regiões sombreadas
57- Área de superfície Determine a área da superfície gerada pela rotação da curva y = x 2 + 2 , 0 ≤ x ≤ 2 , em torno do eixo x .
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.75. y 2 - 4 x = 4e4 x - y = 16
Determine as áreas das regiões compreendidas entre as curvas nos Exercícios 81-84.84. x + y 2 = 3e4 x + y 2 = 0