(a) Use um gráfico de para estimar os valores máximo e mínimo. Então, encontre os valores exatos.
(b) Estime o valor de em que cresce mais rapidamente. Então, encontre o valor exato.
Passo 1
Oiii galerinha, vamos resolver essa juntinhos?
Nos precisamos utilizar um gráfico, correto?Possuimos diversas ferramentas para plotar o mesmo, porém, vamos utilizar a ferramenta mais comum, que e o nosso geogebra, para plotar esse gráfico.
Podemos observar o comportamento da função e estimar os valores máximos e mínimos.
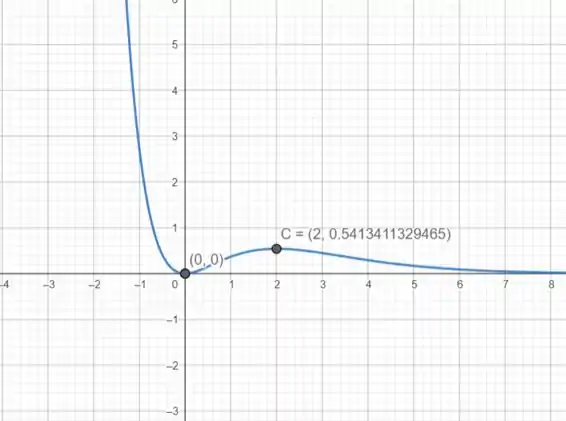
Agora bora resolver essa questão na raça, rsrs or no!
Vamos lá ...
Passo 2
Letra (a): Valores máximo e mínimo de
Para encontrar os pontos críticos:
- Derivamos a função para encontrar os pontos onde a derivada é zero ou não existe.
- A função dada é
- Usamos a regra do produto para derivar
- Igualamos a derivada a zero para encontrar os pontos críticos:
Como para qualquer temos:
Passo 3
Avaliar nos pontos críticos e nos limites do domínio:
- Como tende a zero muito rapidamente à medida que aumenta, também tende a zero quando
- Verificamos os limites quando e
Para a função não é definida (já que explode para infinito enquanto é uma parabólica crescente).
Portanto, o valor máximo exato é e o valor mínimo exato é.
Passo 4
Letra (b): Estimar o valor de em que cresce mais rapidamente
- Observando o gráfico, podemos ver que cresce mais rapidamente próximo ao ponto de inflexão da função antes de atingir o valor máximo.
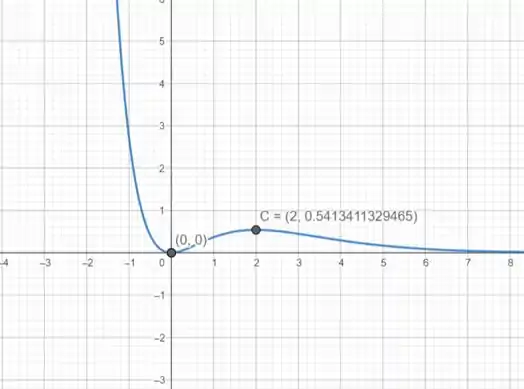
Para encontrar o ponto de inflexão:
- O ponto onde a função cresce mais rapidamente está relacionado com a concavidade da função. Encontramos isso pela segunda derivada.
- Derivamos a primeira derivada
Passo 5
- Igualamos a segunda derivada a zero para encontrar os pontos de inflexão:
Resolvemos a equação quadrática:
- Entre esses pontos, , analisamos a concavidade para determinar onde a função cresce mais rapidamente. para e para
Portanto, a função cresce mais rapidamente em torno de .
Resposta
(a) O ponto de máximo local ocorre em e ponto de mínimo local ocorre em.
(b) cresce mais rápido em .