(a) Encontre as assíntotas vertical e horizontal.
(b) Encontre os intervalos nos quais a função é crescente ou decrescente.
(c) Encontre os valores máximos e mínimos locais.
(d) Encontre os intervalos de concavidade e os pontos de inflexão.
(e) Use a informação das partes (a)-(d) para esboçar o gráfico de .
Passo 1
Oi pessoal, bora resolver essa comigo?
Vamos resolver cada parte da questão para a função
(a) Assíntotas Verticais e Horizontais
Assíntotas verticais ocorrem onde o denominador da função é zero (desde que o numerador não seja zero ao mesmo tempo):
Portanto, há uma assíntota vertical em
Assíntotas Horizontais
Para encontrar as assíntotas horizontais, analisamos o comportamento de quando
Como
Como
Portanto, há uma assíntota horizontal em
Passo 2
(b) Intervalos de Crescimento e Decrescimento
Para determinar os intervalos de crescimento e decrescimento, precisamos encontrar a derivada primeira e analisar os seus sinais:
Usamos a regra do quociente:
Simplificando:
Passo 3
Para encontrar os intervalos de crescimento e decrescimento, analisamos o sinal de
- Para é negativo, e é negativo, então é positivo.
- Para é positivo, e é negativo, então é negativo.
- Para é positivo, e é positivo, então é negativo.
Portanto:
- A função é crescente em
- A função é decrescente em
Passo 4
(c) Valores Máximos e Mínimos Locais
Para encontrar os valores máximos e mínimos locais, analisamos os pontos críticos onde ou não está definida:
Analisando o comportamento em
- Para é positivo.
- Para é negativo.
Portanto, há um máximo local em
Para a derivada não está definida, indicando uma possível descontinuidade.
Passo 5
(d) Intervalos de Concavidade e Pontos de Inflexão
Para determinar os intervalos de concavidade e os pontos de inflexão, precisamos da segunda derivada :
Usamos a regra do quociente novamente para encontrar :
Passo 6
Para determinar a concavidade:
- indica concavidade para cima.
- indica concavidade para baixo.
Analisamos os sinais de
- Para é negativo, e é positivo, então é negativo (concavidade para baixo).
- Para é positivo, e é positivo, então é positivo (concavidade para cima).
Portanto:
- Concavidade para baixo em
- Concavidade para cima em
Passo 7
Pontos de Inflexão
O ponto de inflexão é onde
Portanto, há um ponto de inflexão em
Passo 8
Para plotar o gráfico, temos as seguintes informações descobertas durante a resolução do problema:
Assíntotas:
- Vertical:
- Horizontal:
Intervalos de Crescimento e Decrescimento:
- Crescente:
- Decrescente:
Valores Máximos e Mínimos Locais:
- Máximo local em
Intervalos de Concavidade e Pontos de Inflexão:
- Concavidade para baixo:
- Concavidade para cima:
- Ponto de inflexão:
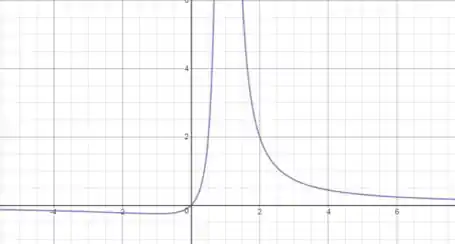
Resposta
Vide o passo a passo.