Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.2 - Ex. 7

Use o gráfico de para estimar os valores de que satisfaçam à conclusão do Teorema do Valor Médio para o intervalo [0, 8].

Passo 1

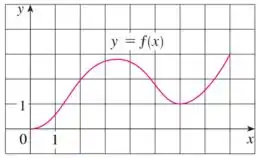
Eaee, belezinha?? Bom... a questão nos dá o seguinte gráfico de uma função :

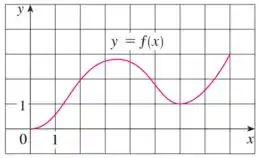
Através desse gráfico, queremos estimar os valores de que satisfaçam à conclusão do Teorema do Valor Médio para o intervalo .

Mas que valores são esses??

Bom... vamos relembrar o Teorema do Valor Médio.

Suponha que seja contínua em um intervalo fechado e diferenciável em um intervalo aberto . Então, existe pelo menos um número no intervalo aberto tal que:

Agora vamos aplicar!! 😉

Passo 2

Trazendo pro nosso caso, temos:

Procuramos um ponto então em que a inclinação da reta tangente ao gráfico é igual a .

Passo 3

Analisando o gráfico, vemos que isso ocorre nos pontos marcados:

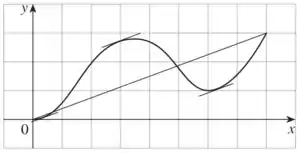
Esses pontos são aproximadamente:

Entendeu direitinho?? Responde aee 😉

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Encontre um intervalo [ a , b ] no qual f x = x 4 + x 3 - x 2 + x - 2 Satisfaz as hipóteses do Teorema de Rolle.(b) Gere o gráfico de f ' ( x ) e use-o para fazer estimativas de todos os valores d

Verifique se as hipóteses do Teorema do Valor Médio estão satisfeitas nos intervalos e encontre todos os valores de c nesses intervalos que satisfazem a conclusão do teorema. f x = x 2 - x ; - 3 , 5

Verifique se as hipóteses do Teorema de Rolle estão satisfeitas nos intervalos e encontre todos os valores de c nesses intervalos que satisfazem a conclusão do teorema. f x = x 2 - x ; [ 0 ,4 ]

Verifique se as hipóteses do Teorema de Rolle estão satisfeitas nos intervalos e encontre todos os valores de c nesses intervalos que satisfazem a conclusão do teorema. f x = x 2 - 8 x + 15 ; [ 3 ,5 ]

Verifique se as hipóteses do Teorema de Rolle estão satisfeitas nos intervalos e encontre todos os valores de c nesses intervalos que satisfazem a conclusão do teorema. f x = l n ⁡ ( 4 + 2 x - x 2 ) ;