Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 26
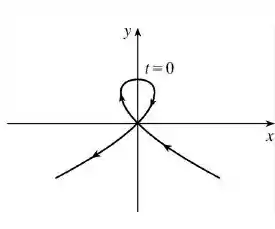
Use os gráficos de
Para esboçar a curva paramétrica
Indique com setas a direção na qual a curva é traçada à medida que aumenta.
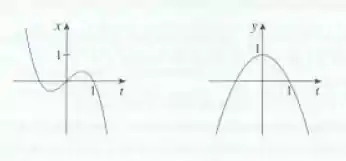
Passo 1
Olhando para os gráficos de e , dá pra ver de cara que quando , temos o ponto
Quando , temos o ponto
Quando temos o ponto
Além disso, quando tanto quanto tendem a diminuir e assumir valores cada vez mais negativos.
E quando , tende a crescer assumindo valores cada vez maiores e positivos e tende a diminuir, assumindo valores cada vez menores (maiores em módulo, porém negativos).
Passo 2
Dito isso, vamos começar plotando os dois pontos que temos certeza:
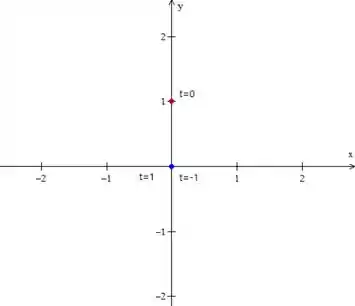
Com isso já da pra gente saber o sentido da curva, certo?
E dai a gente conclui que a curva passa duas vezes no mesmo lugar, ou seja, ela faz um looping na origem.
Acontece que isso e e as outras coisas que dissemos no passo 1 sobre o que acontece quando e quando a gente ainda não consegue saber exatamente como que a curva faz isso, porque nossos dois pontos estão sobre a mesma reta.
Vamos então tentar ver uns outros valores para e com isso achar mais ou menos uns outros pontos , plotar esses pontos e aí sim ver a cara que nossa curva toma.
Passo 3
Vamos olhar nossos gráficos de novo:
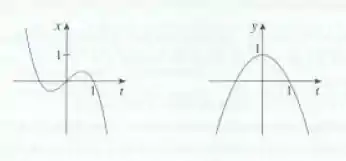
Se pegarmos , temos mais ou menos o ponto
Agora :
Vamos pegar agora :
E, pela simetria, para :
Acho que já tá bom né?
Vamos plotar esses pontos. Vou numerar também a ordem em que a curva tem que passar em cada ponto de acordo com o valor de . Depois a gente liga tudo.
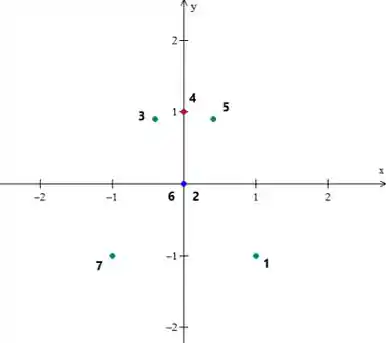
Agora se a gente ligar todos eles, teremos uma curva mais ou menos assim:
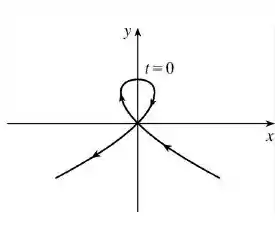
Resposta
